Volume of Solid of Revolution about x-axis. Volume of a Solid of Revolution for a Parametric Curve.

Volume Of Revolution The Disk Method Youtube
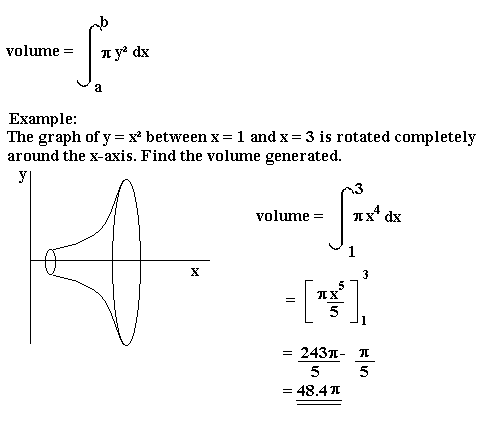
Volumes Of Revolution Mathematics A Level Revision
Volumes Of Revolution Mathematics A Level Revision
To the right is displayed what the solid of revolution would look like if you rotated the displayed area about the x-axis.
Volume of revolution. What is the function. We first must express x in terms of y so that we can apply the volume of solid of revolution formula. The volume of this solid may be calculated by means of integration.
If a bounding curve is defined in parametric form by the equations x xleft t right y yleft t right where the parameter t varies from alpha to beta then the volume of the solid generated by. This is called the volume of revolution. You can also use disk method calculator to learn while doing doing practice online.
01 x2 1 2dx 01 x4 2x2 1 dx. B Show that the volume Of the solid Of revolution formed is given by the integral k sinle de where k is a constant. Given the equation of curve in polar form as rf θ where θ varies from θ 1 to θ 2 the volume of revolution is calculated using the given formulas.
C Hence find the exact value for this volume giving your answer in the form 3 where p and q are constants. The volume of the shape that is formed can be found using the formula. So the volume V of the solid of revolution is given by V lim δx0 Xxb xa δV lim δx0 Xxb xa πy2δx Z b a πy2dx where we have changed the limit of a sum into a definite integral using our definition of inte-gration.
If we want to find the area under the curve y x 2 between x 0 and x 5 for example we simply integrate x 2 with limits 0 and 5. Volumes of Revolution About this Lesson This lesson provides students with a physical method to visualize 3-dimensional solids and a specific procedure to sketch a solid of revolution. Common methods for finding the volume are the disc method the shell method and Pappuss centroid theorem.
A Cone Take the very simple function yx between 0 and b. A solid of revolution is a three-dimensional object obtained by rotating a function in the plane about a line in the plane. We can use the same strategy to find the volume that is swept out by an area between two curves when the area is revolved around an axis.
The volume V of a solid generated by revolving the region bounded by y fx and the xaxis on the interval a b about the xaxis is. We can think of the volume of the solid of revolution as the subtraction of two volumes. For example the volume of revolution of the curve y x2 1 about the x -axis between x 0 and x 1 is.
V 2 3 π x 2 2 d x V π 2 3 x 4 d x V π 1 5 x 5 2 3 V π 243 5 32 5 V 55 π. Find volume of solid of revolution step-by-step. In other words to find the volume of revolution of a function fx.
Students determine the perimeter and area of two-dimensional figures created by graphing equations on a coordinate plane. We have seen how to find the area between two curves by finding the formula for the area of a thin rectangular slice then integrating this over the limits of integration. 5x5 32x3 x1 0 51 32 1 1528.
The volume of a solid revolution by disk method is calculated as. Volume of a solid of revolution generated by rotating two curves around the x axis Formula 3 - Disk around the y axis If z is a function of y such that x zy and zy 0 for all y in the interval y1 y2 the volume of the solid generated by revolving around the y axis the region bounded by the graph of z the y axis x 0 and the horizontal lines y y1 and y y2 is. Its volume is calculated by the formula.
To use the calculator one need to enter the function itself boundaries to calculate the volume and choose the rotation axis. If the region bounded by x fy and the yaxis on a b is revolved about the yaxis then its volume V is. In this section the first of two sections devoted to finding the volume of a solid of revolution we will look at the method of ringsdisks to find the volume of the object we get by rotating a region bounded by two curves one of which may be the x or y-axis around a.
This formula now gives us a way to calculate the volumes of solids of revolution about the x-axis. Our online calculator based on Wolfram Alpha system is able to find the volume of solid of revolution given almost any function. If y x 3 then x y 13 The formula requires x 2 and on squaring we have x 2 y 23.
Adjust the a and b values by using either the sliders or entering them in the input boxes yourself. Integrate pi times the square of the function. Now imagine that a curve for example y x 2 is rotated around the x-axis so that a solid is formed.
Enter in the function in the blue input box below. X msquare log_ msquare sqrt square nthroot msquare square le. The outer volume is that of the solid of revolution created by rotating the line yx around the x-axis see left graph in the figure below namely the volume of a cone and the inner volume is that of the solid of revolution created by rotating the parabola yx2 around the x-axis see right graph in the figure below.
4a Volume Of Solid Of Revolution By Integration Disk Method
6 2 Volume Of Solid Of Revolution
Volume Of A Solid Of Revolution

Volumes Of Solids Of Revolution Ppt Download

Formula Derivation For Volume Of Cone Revolution Of Solids Calculus Integration Youtube
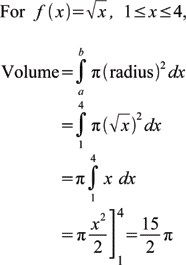
Volume Of A Solid Of Revolution

Solids Of Revolution Volume Project 1ntegration By Parts

Volumes Of Solids Of Revolution Advanced Higher Maths
